نظريات ومبرهنات فيتاغورس

وهي الشكل الأكثر شهرة لنظرية فيثاغورس:/

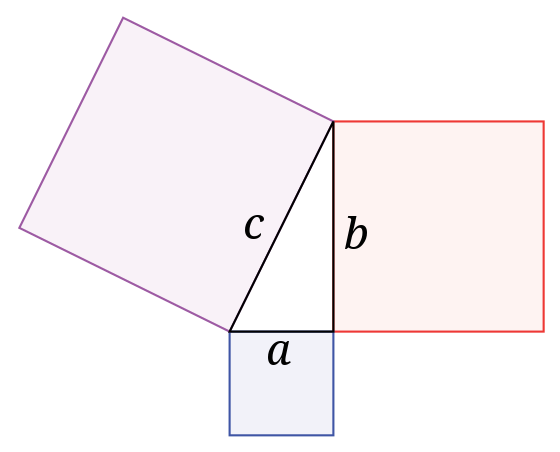
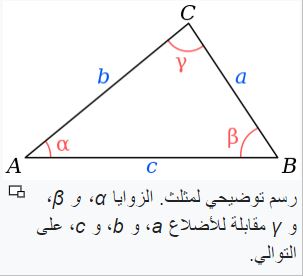
« في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة. »

 في مثلث ABC قائم الزاوية في C، أي أن [AB] هو الوتر، نضع AB=c و AC=b و BC=a. لدينا:/

{displaystyle BC^{2}+AC^{2}=AB^{2},}{displaystyle BC^{2}+AC^{2}=AB^{2},}

أو

{displaystyle a^{2}+b^{2}=c^{2},}{displaystyle a^{2}+b^{2}=c^{2},}

تمكن نظرية فيثاغورس من حساب طول أحد أضلاع مثلث قائم الزاوية بمعرفة طولي الضلعين الآخرين. مثلا:/ إذا كان b=3 و a=4 فإن

{displaystyle a^{2}+b^{2}=3^{2}+4^{2}=25=c^{2},}{displaystyle a^{2}+b^{2}=3^{2}+4^{2}=25=c^{2},}

ومنه {displaystyle c=5,}{displaystyle c=5,}.

أي ثلاثة أعداد صحيحة تمثل أطوال أضلاع مثلث قائم الزاوية -مثل (3، 4، 5)- تُكون ثلاثي فيثاغورسي.

عرفت خاصية فيثاغورس في العصور القديمة، والدلائل على ذلك ما زالت موجودة حتى الآن. يكفي مثلا أن نلاحظ الحبل ذا ثلاث عشرة عقدة الذي كان المسّاحون المصريون يستعملونه والذي نجد له صورا في عدة تصاوير للأعمال الزراعية. يسمح هذا الحبل، علاوة على قياس المسافات، بإنشاء زوايا قائمة دون الحاجة إلى جيب التمام، إذ تسمح العقد الثلاث عشرة (والمسافات الاثنتي عشرة الفاصلة بين العقد) من إنشاء مثلث أبعاده (5 ،4 ،3)، مثلث يتضح أنه قائم الزاوية. ظل هذا الحبل أداة هندسية طيلة العصور الوسطى.

أقدم تمثيل لمثلوثات فيثاغورس (مثلث قائم الزاوية وأطوال أضلاعه أعداد صحيحة طبيعية) نجده في الميغاليثات (2500 سنة قبل الميلاد). كما أظهرت آثار البابليين (لوحة Plimpton، حوالي سنة 1800 قبل الميلاد) أنه قبل ظهور فيثاغورس بأكثر من 1000 سنة، عرف المهندسون وجود مثلوثات فيثاغورس.

لكن بين اكتشاف الخاصية «نلاحظ أن بعض المثلثات القائمة الزاوية تحقق هذه الخاصية»، تعميمها «يبدو أن كل المثلثات القائمة الزاوية تحقق هذه الخاصية» وإثباتها «كل المثلثات القائمة الزاوية (فقط) في المستوى الإقليدي تحقق هذه الخاصية» عدة أجيال.